Modul: Grafik
| Website: | ORCA.nrw |
| Kurs: | Grundwissen: Datenmanagement in Studium & wissenschaftlicher Praxis |
| Buch: | Modul: Grafik |
| Gedruckt von: | Gast |
| Datum: | Freitag, 18. April 2025, 16:26 |
Über dieses Modul
Hier erfahren Sie etwas über
- die Rastergrafikformate TIFF, JPEG, JPEG 2000
- das Vektorgrafikformat SVG
Lernziel: (Wissen): Die Studentinnen und Studenten kennen einige im Forschungsbereich weit verbreitete Grafikformate.
Lernziel: (Verstehen): Die Studentinnen und Studenten können ein für den jeweiligen Zweck zumindest grundsätzlich geeignetes Grafikformat auswählen.
Bearbeitungsdauer: ≈ 35 Min.
Rastergrafiken
Unterscheidung von Raster- und Vektorgrafiken
Es gibt zwei Arten von digitalen Grafiken, Rastergrafiken und Vektorgrafiken. In einer Rastergrafik liegt das Bild gerastert vor, d.h. in Pixel gleicher Größe zerlegt. Abgespeichert werden Rastergrafiken meist block- oder streifenweise in einer Datei. Die eigentlichen Bilddaten sind nicht zeichencodiert, weil das Datenvolumen bei Verwendung von Text viel zu groß wäre.
Vektorgrafiken unterscheiden sich deutlich von Rastergrafiken. Eine Vektorgrafik ist aus geometrischen Grundelementen aufgebaut, z.B. Rechteck und Kreis. Die Lage des Grundelements wird durch einen Vektor festgelegt. Wesentliche Unterschiede sind in der Tabelle zusammengestellt.
| Rastergrafik | Vektorgrafik |
|
|---|---|---|
| Enthält was? |
Pixel gleicher Form und Größe |
Geometrische Objekte, wie z.B. Rechtecke und Kurven |
| Wie angeordnet? |
In einem festen Raster aneinandergesetzt |
Mittels einer Ortsangabe (Vektor) einem beliebigen Ort innerhalb der Grafik zugeordnet |
| Überlappungen | Nein, Pixel überlappen sich nicht | Möglich, Objekte einer Vektorgrafik können sich überlappen |
| Skalierbarkeit | Pixel werden bei erheblicher Vergrößerung sichtbar |
Vektorgrafik lässt sich beliebig vergrößern (ist "beliebig skalierbar") |

Rastergrafik, die wegen starker Vergrößerung pixelig erscheint
Vektorgrafiken werden bei Vergrößerung nicht pixelig, sondern sind beliebig skalierbar. Das gilt sogar für Farbverläufe. Klicken Sie auf den Regenbogen.
TIFF
TIFF (Tagged Image File Format) ist ein Rastergrafikformat, das schon vor Jahrzehnten von Aldus und Microsoft entwickelt worden ist. Die aktuelle Version 6.0 stammt von 1992. TIFF kommt ohne Kompression aus und ermöglicht die Speicherung von gerasterten Bildern ohne Informationsverlust. Es stehen bei Bedarf aber auch verschiedene Kompressionsalgorithmen zur Verfügung.
Merke! Unkomprimiertes TIFF ist als langzeitstabiles und offenes Dateiformat für die verlustfreie Langzeitspeicherung von Rastergrafiken sehr gut geeignet.
TIFF-Dateien bestehen aus einem Header und einem binären (nicht textkodierten) Datenteil mit dem kodierten Bild. Im Header sind Titel, Farbmodell, Größe, Auflösung und weitere Bildparameter ebenfalls binär abgelegt.
Daneben ist es aber auch möglich, in den Header normalen ASCII-Text in Metadatenfelder hineinzuschreiben. Die Metadaten-Textfelder können zu Dokumentationszwecken genutzt werden. Beispielsweise schreiben viele Kameras dort automatisch Geräteinformationen hinein.
TIFF kann in der Regel von Web-Browsern nicht dargestellt, sondern nur unter Zuhilfenahme weiterer Software geöffnet werden. Dennoch ist es weit verbreitet, z.B. in Verlagen und Druckereien, die gern die Erweiterung TIFF-CMYK nutzen. Durch das hier verwendete CMYK-Farbmodell ist TIFF-CMYK als Druckvorstufe für den Vierfarbdruck bestens geeignet. Es gibt noch zahlreiche andere TIFF-Erweiterungen. Für den wissenschaftlichen Gebrauch sind vor allen die folgenden von Bedeutung:
| geoTIFF und COG |
für die Einbettung georeferenzierter Informationen in TIFF (COG steht für "Cloud Optimized geoTIFF") |
|---|---|
| BigTIFF | für große Bilddateien (mehr als 4 GB), wie sie z.B. in der Astronomie erzeugt werden |
| TIFF-LZW | für verlustfrei komprimierte TIFF-Bilder (Lempel-Ziv-Welch-Algorithmus) |
Eine unkomprimierte TIFF-Datei zum Ausprobieren: Carmen009.tif (5.56 MB).
JPEG
JPEG ist ein üblicherweise verlustbehaftetes Rastergrafikformat, d.h. bei der Speicherung in diesem Format gehen Bildinformationen verloren.
Merke! JPEG ist daher nicht für die Langzeitspeicherung von Forschungsdaten geeignet. Dennoch besitzt es Bedeutung im Forschungsdatenmanagement, und zwar dann, wenn Bilddaten über das Web in kürzester Zeit verfügbar gemacht werden sollen, da es sehr gute Kompressionsmöglichkeiten bietet, sogar für Fotos. Je größer eine Datei ist, desto länger ist auch die Übertragungszeit im Netzwerk. Die verglichen mit unkomprimiertem TIFF viel kleineren JPEG-Dateien können schneller über das Web übertragen werden und eignen sich daher als Previews und für Webseiten allgemein.
Ein Preview befindet sich häufig auf der Landungsseite eines Forschungsdatensatzes im Repositorium. Große Bedeutung besitzt es beispielsweise bei digitalen Editionen. HTML-Seiten mit eingebauten JPEG-Bildern erleichtern Orientierung und Auswahl bei der Nachnutzung. Für die Detailforschung müssen die verlustfrei gespeicherten Bilddaten jedoch zusätzlich bereitgehalten werden, z.B. über eine Download-Möglichkeit.
JPEG eignet sich auch für die Visualisierung umfangreicher numerischer Daten, beispielsweise von Simulationsdaten. Einige Forschungsdatenrepositorien ermöglichen das durch Software, die die Daten auf dem Server einliest und daraus ein (möglicherweise relativ grobes) Bild erzeugt. Die Detailforschung findet dann meist wieder auf den lokalen Rechnern der Forschenden unter Verwendung der heruntergeladenen Forschungsdaten statt.
Erzeugung von JPEG
In einer JPEG-Datei sind die Bildinformationen auf völlig andere Weise gespeichert als in einer TIFF-Datei. Mehrere Einzelschritte werden benötigt, um aus den gerasterten Bilddaten JPEG-Daten zu berechnen:
- Zunächst wird die Farbinformation bearbeitet. Der wichtigste Teilschritt ist
die Fortlassung der Farbinformation an jedem zweiten Pixel sowohl in x-
und auch in y-Richtung. Insgesamt wird so 3/4 der Farbinformation
eingespart. Die Vorgehensweise wird Unterabtastung
genannt. Das menschliche Auge erkennt den Unterschied nicht, weil die
Farbsehschärfe geringer ist als Hell-Dunkel-Sehschärfe. Dies liegt
daran, dass die Stäbchenzellen, die für das Hell-Dunkel-Sehen
verantwortlich sind, viel häufiger in der Netzhaut vorkommen als die
Zapfen, die uns das Farbsehen ermöglichen.
- Das Graustufen-Rasterbild wird in Quadrate zerlegt, die alle eine Größe von 8x8 Pixeln besitzen.
- Innerhalb der Quadrate werden die Graustufen der 64 Pixel auf 64 Koeffizienten von 64 Basisbildern umgerechnet.
- Wie die Basisbilder
aussehen, zeigt die Grafik. Jeder der roten Kästen enthält ein
Basisbild. Die Basisbilder besitzen ebenfalls die Größe von 8x8 Pixeln
und sind aus den Cosinusfunktionen entstanden, die als blaue Kurven in
der oberen Zeile für die x-Richtung bzw. in der ersten Spalte für die
y-Richtung gezeigt sind. Da Rasterbilder nur pixelweise definiert sind,
werden die Cosinusfunktionen abschnittsweise über die Pixellänge
gemittelt. Es resultieren die Treppenfunktionen, die in Zeile 2 bzw.
Spalte 2 als Blockdiagramme dargestellt sind ("diskretisierte"
eindimensionale Funktion).
- Im zweidimensionalen Basisbild wurden die Grauwerte Pixel für Pixel durch Multiplikation der Werte der zugehörigen diskretisierten eindimensionalen Funktionen berechnet.
- Die zweidimensionalen Basisbilder sind in Grauwerten dargestellt. Hell bedeutet einen hohen, dunkel einen niedrigen (negativen) Wert. Null entspricht einem Mittelgrau.
- Wie werden nun die 64 Koeffizienten berechnet, die für die Speicherung
gebraucht werden?
Für jeden Koeffizienten werden drei Schritte benötigt:
- 8x8-Quadrat und Basisbild werden übereinandergelegt,
- die Grauwerte der übereinander liegenden Pixel multipliziert und
- alle diese Produkte aufsummiert.
- Eines der Basisbilder unterscheidet sich deutlich von den anderen 63, der
Gleichanteil links oben.
Es ist anders als die 63 Wechselanteile überall gleich hell. Multipliziert mit seinem Koeffizienten ist er die mittlere Helligkeit des Bildes.
- Die Wechselanteile ändern sich hingegen periodisch.
Sie besitzen Frequenzen in zwei Raumrichtungen, eine in x-Richtung, die andere in y-Richtung.
- Aus den 64 Koeffizienten kann das ursprüngliche 8x8-Pixelquadrat wieder
berechnet werden. Die Animation rechts zeigt am Beispiel des
Buchstaben H in der Vergrößerung, wie das geschieht.
Starten Sie die Animation, indem Sie die Maus in den Rahmen ziehen.
Wegziehen beendet die Animation.
Die Basisbilder in den roten Quadraten werden mit den zugehörigen Koeffizienten multipliziert. Die Teilsummen werden im mittleren Quadrat gezeigt. Die bereits verarbeiteten Basisbilder sind in der Übersicht darüber rot umrandet. Die Summe wird dem Bild vor der Kodierung immer ähnlicher. Basisbilder mit kleinen Koeffizienten tragen zum Gesamtbild jedoch nur wenig bei. Im animierten Beispiel ist die Hälfte der Koeffizienten sogar 0, da H spiegelsymmetrisch ist und deshalb nur aus spiegelsymmetrischen Basisbildern aufgebaut sein kann.
- Wie die Basisbilder
aussehen, zeigt die Grafik. Jeder der roten Kästen enthält ein
Basisbild. Die Basisbilder besitzen ebenfalls die Größe von 8x8 Pixeln
und sind aus den Cosinusfunktionen entstanden, die als blaue Kurven in
der oberen Zeile für die x-Richtung bzw. in der ersten Spalte für die
y-Richtung gezeigt sind. Da Rasterbilder nur pixelweise definiert sind,
werden die Cosinusfunktionen abschnittsweise über die Pixellänge
gemittelt. Es resultieren die Treppenfunktionen, die in Zeile 2 bzw.
Spalte 2 als Blockdiagramme dargestellt sind ("diskretisierte"
eindimensionale Funktion).
- JPEG erreicht eine besonders gute Kompression, indem ausgenutzt wird, dass die Wechselanteile mit hohen Frequenzen durch unseren Sehsinn weniger gut wahrgenommen werden können. Das gilt insbesondere für die Anteile mit hohen Frequenzen in beiden Raumrichtungen. "Kleinkariert" ist einer Wahrnehmung nicht nur im übertragenen Sinne nicht förderlich, sondern auch ganz direkt nicht. JPEG verringert den Speicherbedarf, indem die Koeffizienten quantisiert werden. Die Quantisierung ist ein denkbar einfaches Verfahren. Bei der Quantisierung wird der Koeffizient durch einen vorher willkürlich festgelegten Tabellenwert, den Q-Wert, dividiert und anschließend auf die nächste ganze Zahl gerundet. Der Q-Wert berücksichtigt die schlechtere Wahrnehmbarkeit der hochfrequenten Anteile. Der Q-Wert ist umso höher, je höher die Frequenzen in den beiden Raumrichtungen sind und je höher der Nutzer die Kompressionsrate eingestellt hat. Bei der Quantisierung werden die Koeffizienten vieler weniger bedeutender Wechselanteile auf null gerundet. Die vielen Nullen ermöglichen eine weitere erhebliche Platzersparnis.
- Durch Umsortierung der Basisbilder bzw. der zugehörigen Koeffizienten wird ein Vektor erzeugt. Die Abbildung zeigt, wie umsortiert wird.
Dabei finden sich die hochfrequenten Basisbilder hinten wieder. Das sind sehr häufig die weniger bedeutenden, so dass die Nullen nach der Umsortierung meist hinten stehen. Die Nullen am Ende müssen nicht abgespeichert werden, sondern nur die Werte bis zum letzten Wert ungleich null. Dahinter folgt nur noch die Blockende-Markierung. Auch die übrigen Werte werden platzsparend gespeichert.
Unterabtastung und Quantisierung führen zu Informationsverlusten. Selbst wenn diese für uns Menschen oft nicht sichtbar sind, wird die maschinelle Verarbeitbarkeit der Bilder durch die Verluste dennoch eingeschränkt. In der obigen Animation lassen sich beispielsweise in einiger Entfernung vom Buchstaben H auch dann noch graue Flecken ausmachen, wenn nur noch wenige Basisbilder bis zur vollständigen Aufsummierung fehlen.
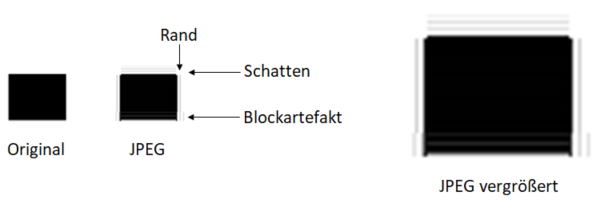
Wenn die Kompression zu weit getrieben wird, werden auch für uns Menschen im Bild Artefakte sichtbar, insbesondere an harten Kontrasten. Das können Ränder, Schatten oder Blockartefakte sein, die hier am Beispiel eines übertrieben komprimierten Rechtecks gut zu erkennen sind.
Wenn mit den Default-Einstellungen von Grafikprogrammen und Formatkonvertierungs-Tools gearbeitet wird, sollten solche sichtbaren Artefakte aber nicht entstehen. Dennoch ist die Konvertierung zu JPEG immer mit einem Informationsverlust verbunden. Bildinformation geht vor allem bei der Unterabtastung und der Quantisierung verloren. Verlustfrei arbeitende JPEG-Varianten sind zwar zusammen mit den verlustbehafteten spezifiziert worden, sie haben sich aber nicht durchgesetzt und werden nicht genutzt.
Hinweis: Zur Erzeugung von JPEG wird es im Abschlussquiz keine Fragen geben.
JPEG 2000
Das leistungsstarke JPEG 2000 greift die Ideen auf, die zum JPEG-Format führten, nutzt aber neuere mathematische Verfahren und arbeitet mit Waveletts statt mit Cosinusfunktionen. Waveletts, übersetzt "Wellchen", sind nur auf einem beschränkten Intervall ungleich null. Durch diese Fokussierung können die Bilder in der verlustbehafteten Variante von JPEG 2000 noch stärker komprimiert werden als JPEG, bis Bildartefakte deutlich sichtbar werden. Die verlustbehaftete Variante arbeitet wie JPEG mit einer Quantisierung.
Es gibt aber auch eine verlustfrei arbeitende Variante, die verglichen mit dem unkomprimierten Bild auch schon eine gewisse Kompression ermöglicht und ohne Quantisierung auskommt. Die Patentierung eines Teils der Technik hat eine weite Verbreitung von JPEG 2000 bisher leider verhindert.
Testaufgabe
Vektorgrafikformat SVG
Ein verbreitetes Vektorgrafik-Format ist SVG (Scalable Vector Graphics). SVG ist eine in XML kodierte und vom World Wide Web Consortium (W3C) empfohlene Auszeichnungssprache für zweidimensionale Vektorgrafiken. Moderne Web-Browser können SVG darstellen, wobei die SVG-Grafiken noch nicht einmal in separaten Dateien vorliegen müssen. SVG kann direkt in HTML hineingeschrieben werden ("inline").
Merke! SVG eignet sich sehr gut für die Langzeitarchivierung von Forschungsdaten. Einige Gründe:
- SVG ist aufgrund der W3C-Empfehlung langfristig lesbar und im Web weit verbreitet
- SVG ist öffentlich zugänglicher Standard und entgeltfrei nutzbar
- Als XML-Auszeichnungssprache ist SVG menschen- und maschinenlesbar. Beispielsweise lässt es sich per Volltextsuche und mit normalen Text-Suchmaschinen durchsuchen
- SVG kann verlustfrei gespeichert werden
- SVG ist platzsparend, sofern nicht versucht wird, eine Rastergrafik als Vektorgrafik zu speichern mit den Pixeln als Elementen
Eine Einführung in SVG mit Nachschlagewerk finden Sie in selfhtml.
Erzeugung
SVG kann mit einem einfachen Texteditor oder mit Zeichenprogrammen erzeugt werden. Ein Open-Source-Programm, das in SVG und vielen anderen Formaten abspeichern kann und zudem entgeltfrei ist, ist Inkscape. Der Screenshot zeigt die Benutzeroberfläche von Inkscape mit Farbpalette und Werkzeugauswahl.
Für die Arbeit mit Inkscape sind SVG-Kenntnisse nicht unbedingt erforderlich. Nützlich sind sie jedoch.
Objekte
In einer SVG-Grafik bestimmt ein Ortsvektor die genaue Lage des Objekts. Der Koordinatenursprung befindet sich — wenn nichts anderes bestimmt wurde — am linken oberen Bildrand. Ist das Grafikobjekt ein Rechteck, zeigt der Ortsvektor auf die linke obere Ecke des Rechtecks. Beim Kreis und Ellipse ist es der Mittelpunkt (cx,cy), der die Lage bestimmt. Das "c" ist keine mathematische Konstante, sondern steht für "circle".
Die Objekteigenschaften sind durch Attribute spezifiziert, z. B. Breite und Höhe beim Rechteck sowie der Radius beim Kreis. Die Ellipse wird durch zwei Radien festgelegt. Die Tags für Kreis und Ellipse aus der Abbildung lauten ohne Attribute für Farbe und Rand:
<circle description="Beispielkreis" cx="200" cy="250" r="100"/>
<ellipse description="Beispiel-Ellipse" cx="800" cy="300" rx="120" ry="70"/>
Die Abbildung unten zeigt drei Beispiele für Rechtecke und die Attribute, die die Lage und Form spezifizieren. Das magentafarbene Rechteck ist kreisförmig gerundet und das grüne Rechteck ellipsenförmig gerundet. Dies wird durch die Angabe von Rundungsradien rx und ry größer als null erreicht. rx und ry sind die Radien der Ellipse in x- und in y-Richtung, nach denen die Rundung ausgeformt wird. Sind rx und ry gleich, so ist die Ellipse ein Kreis und die Rundung folgerichtig kreisförmig.
Neben Pflichtangaben zur Festlegung der Objektform gibt es eine Fülle optionaler Attribute, beispielsweise für die Füllfarbe und die Farbe und Strichstärke des Randes. So wird das hellblaue Rechteck erzeugt durch
<rect x="50" y="10" width="200" height="100" fill="lightblue" stroke="black" stroke-width="1"/>
Dabei steht stroke für den Rand des Rechtecks bzw. allgemein für den Rand eines beliebigen Grafikelements. Der Wert von stroke ist die Farbe des Randes. Ohne die Angabe der Farbe wird kein Rand gezeichnet.
Das ist bei der Füllfarbe anders. Wird fill="..." weggelassen, wird schwarz gefüllt.
Neben Rechteck, Kreis und Ellipse kennt SVG Pfade und Text. Pfade gibt es als einfache Linie, Polygonzug, elliptischen Bogen und Bézier-Kurve.
SVG-Datei zum Ausprobieren: Nutzer.svg